MATEMATIKA
Borka Marinković
Arhimed
Ne dirajte moje krugove!
 Arhimed, najveći intelektualac drevnih vremena, ne samo da bi se izvanredno razumeo sa Njutnom, već bi se, da je bio savremenik Anštajna, Bora, Hajzenberga i Dirka, verovatno bolje snalazio u matematici i od njih samih. Arhimed, najveći intelektualac drevnih vremena, ne samo da bi se izvanredno razumeo sa Njutnom, već bi se, da je bio savremenik Anštajna, Bora, Hajzenberga i Dirka, verovatno bolje snalazio u matematici i od njih samih.
O svireposti rimskih legionara govore postupci vojnika koji su, pregazivši Arhimedov leš, ušli u njegovu sobu i zgrabili papiruse sa vrednim rezultatima sa stola misleći da su u njima zlatnici. Otimajući se oko listova, vojnici su ih iscepali.
Drugi su uzeli zemljani ćup sa peskom, verujući da je pun zlata.
Ni njegov grob nije bio pošteđen pa njegovi poštovaoci nisu smeli da ga održavaju. Grob je kasnije pronašao Ciceron, i to zahvaljujući crtežu lopte , valjka i kupe koji se nalazio na spomeniku iznad nekoliko stihova urezanih velikom matematičaru u spomen. Kada je raščišćen korov i pošto je prokrčen put, podnožju stuba ukazao se spomenik sa uklesanim natpisom.
Sam crtež na nadgrobnom spomeniku je ilustracija jedne od Arhimedovih najomiljenijih teorema iz stereometrije (geometrije u prostoru). Ovo otkriće, koje se može dobiti iz osobine ravnoteže, objasnio je u svom čuvenom delu :"O sferi i cilindru". Teorema glasi: "Količnik zapremina pravog kružnog cilindra, čija je visina jednaka njegovom prečniku i sfere upisane u taj cilindar, iznosi 3:2, što je jednako količniku njihovih površina".
Zapremine kupe, sfere i cilindra ovih dimenzija su u razmeri 1:2:3.
Arhimedovi radovi iz geometrije bili su značajni ne samo za ondašnje generacije matematičara već su aktuelni i danas.
Neverovatno je do kojih je preciznih rešenja došao Arhimed priborom kojim se služio. Pošto su u njegovo vreme hartija-papirus i voštane tablice bile retka i skupocena roba, Arhimedov sto je imao tri noge i crnu kamenu ploču. Na stolu se nalazio zemljani ćup, napunjen čistim belim peskom. Arhimed bi, pomoću sita, posuo kamenu ploču stola ravnomerno tankim slojem peska da bi mogao da po njoj piše i crta. Lenjir mu je predstavljala jedna široka uglačana letva sa držačem na sredini , a šestar takođe letva koja se obrtala oko teškog olovnog oslonca i imala pokretnu drvenu pisaljku. Kada je hteo da nacrta pravu liniju, Arhimed je polagao lenjir na pesak i povlačio drvenu pisaljku duž njega. Po sklanjanju lenjira, ostajao je jasan crni trag. Na sličan način koristio je šestar. Rešivši postavljeni problem, svoje crteže u pesku brisao je četkom pa je, posuvši ploču ponovo peskom, mogao da crta nove.
Svođenje na apsurd
Arhimed je najveću slavu stekao svojim raspravama o zaobljenim geometrijskim telima, čiju je površinu i zapreminu izračunavao složenom metodom bliskom današnjem infinitezimalnom računu. Taj metod je poznat kao ekshaustija, čija je suština iscrpljivanje s gornje i donje strane i dolaženje, preko pogrešnih vrednosti, do moguće tačnog ishoda. Taj metod je Arhimed razvio najverovatnije na osnovu Demokritove teorije "geometrijskog atoma". Danas je taj metod poznat pod imenom "Svođenje na apsurd"(Reducio ad apsurdum).
“Eureka”
Po rasejanosti, Arhimed je nadmašio i Njutna. Njegova čuvena izreka "Eureka, eureka!" (Otkrio sam, otkrio sam), koju je uzviknuo istrčavši na ulicu iz gradskog kupatila, potpuno nag i sa željom da svoje najnovije otkriće odmah podeli sa okolinom, pokazuje koliko je Arhimed živeo za matematiku. |
Dobar je za proveru i dokazivanje rezultata (poznatog ili pogođenog), ali nije pogodan za nalaženje novog još uvek nepoznatog rešenja.
Arhimed je napravio metod za izračunavanje broja π ( 3 1/7 < π<3 7/71), osmislio je sistem stepenovanja za predstavljanje veoma velikih brojeva. Takođe, bio je jedan jedan od prvih naučnika koji je primenio matematiku na fizičke pojave, začetnik je hidrostatike i statike, uključujući zakon poluge. Zaslužan je za projektovanje mnogo inovativnih sprava koje su primenjene za odbranu od rimskih osvajača.
Profesor Hejberg, priređivač radova o Arhimedu, 1906. otkrio je Arhimedov davno izgubljeni rad pod naslovom "Metod" koji sadrži elemente modernog integralnog računa.
Zameranje pomoću bikova
Arhimed nije imao mnogo simpatija za svog savremenika, velikog matematičara Apolonija. Negativan međusobni odnos je bio obostran. Parodirajući naslov Arhimedovog spisa: "Merenje kruga" i dostignuća objavljena u njemu, Apolonije je napisao delo originalnog naslova:"Sredstvo za ubrzanje porođaja". Arhimed mu je uzvratio tako što je, u jednom zadatku upićenom Erastotenu, napisanom savršenim epskim jonskim jezikom, apostrofirao Apolonija. Problem koji je postavio Arhimed, vezan za broj bikova na ispaši, zaista je za ondašnje doba bio praktično nerešiv jer se odnosi na velike brojeve.
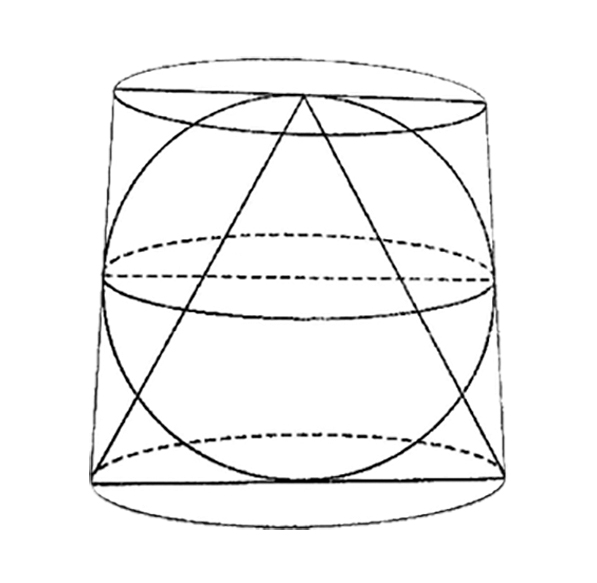
Crtež sa spomenika
|
"Koliko u Sunca krava i bikova ima, izračunaj, stranče,
Napregnuvši um, ako ti je zaista svojstvena mudrost.
...Ako izračunaš koliko je tamo bilo stoke,
koliko je na livadama paslo mesnatih bikova,
koliko krava muzara i koliko od svake boje,
niko te više neće nazvati neznalicom,
ali ni u mudrace te neće ubrojiti.
Ako uz to ne izračunaš i različite navike bikova,
ako se pomešaju crni bikovi sa belim stadom,
oni će u polju zauzeti pravi kvadrat
širine jednake dužini, i ova bezbrojna masa
popuniće čitavo polje Trinakije.
Ako se pokupe zajedno svi mrki i šareni
(a ostali će zasebno pasti,
ili je isto ako im dođu i svi ostali),
tako da u prednjem delu stane jedan, a zatim
u svakom daljem redu sve više, imaće figura,
koju svi oni popunjavaju, tri strane.
Umeš li sve to da nađeš i duhovnim pogledom
da obuhvatiš veličinu stada i drugima da preneseš,
gordo koračaj napred, kiteći se velikom pobedom:
znaj da si, prevazišavši druge, po mudrosti prvi!"
Ovde je reč o složenom problemu; izražen sadašnjim matematičkim alatima, problem izgleda:
t2- 4 729 494u2=1.
Rešenje bi bio broj sa 206.545 decimala, za čiji zapis bi bilo potrebno više od 60 strana.
Srebro a ne zlato
Kako je Arhimed primenio svoje otkriće da bi utvrdio kvalitet materijala od kojih je izrađena kraljeva kruna.
Kralj Sirakuze Hijeron II naručio je da mu se izradi zlatna kruna.
Urađena je izuzetno lepa kruna, sa mnogo zlatnih listića. Podsećala je na lovorov venac. Iako mu se dopala, posumnjao je da je, delimično, umesto zlata, upotrebljeno srebro za njenu izradu. Nezadovoljan, pozvao je svog rođaka, tada najcenjenijeg naučnika Sirakuze u pomoć.
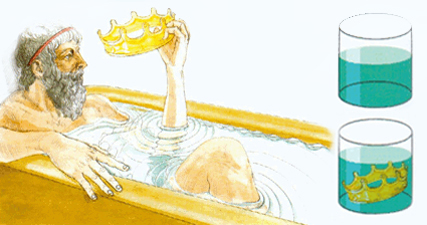
Arhimed je pokušao da reši problem tako što će izmerene težine svih njenih delova podeliti izračunatom zapreminom, čime bi dobio specifičnu težinu koja bi trebalo da bude jednaka specifičnoj težini zlata. Međutim, pošto je kruna imala mnogo nepravilnih delova, izračunavanje zapremine se pokazalo kao veoma složen zadatak koji bi mogao da dovede do pogrešnog rezultata.
Posle dugog razmišljanja odlučio je da primeni svoje otkriće po kojem svako telo uronjeno u tečnost gubi od svoje težine onoliko koliko iznosi težina istisnute tečnosti. Krunu je potopio u vodu, izvršio potrebna merenja i utvrdio da, pri izradi krune, nije korišćeno srebro. Kralj je bio zadovoljan, a majstor je ostao živ.
“Merenje kruga”
Prva žena matematičar je bila Hipatija, iz Aleksandrije. Njen doprinos matematici sastoji se iz mnoštva radova. Zaslužna je za to što je Arhimedovo delo "Merenje kruga" ugledalo svetlost dana, a koje je izvor kasnijeg prevoda na arapski i latinski.
Matematičar i pisac iz regiona Ranko Risojević, u knjizi "Veliki matematičari", pisao je i o Arhimedu i njegovim izuzetnim naučnim dostignućima.
Smrt uz krugove
Vrhunac njegove odanosti nauci potvrđuje opis njegove smrti koja je poznata zahvaljujući Plutarhovom životopisu rimskog vojskovođe Marka Klaudija Marcela. Istina, postoje dve verzije kako je završio Arhimed, ali obe dokazuju da je za nauku moguće dati i život. Po jednoj, posle dvogodišnje opsade Sirakuze, u kojoj je rođen i u kojoj je živeo veliki matematičar, jedan rimski vojnik upao je u dvorište Arhimedove kuće. Zanet nad svojim crtežima na pesku, Arhimed mu se nije poklonio. Ljut zbog ignorisanja, vojnik ga je ubio. U ropcu, Arhimed je uzviknuo: "Noli turbare circulus meos!" ( Ne razarajte moje krugove).

Broj pi
Godine 2019, na predavanju o površini kruga, profesor objašnjava broj π. Sa divljenjem govori o Arhimedu i njegovoj posvećenosti naučnom radu - čak i u slučaju smrtne opasnosti. Učenik je pažljivo slušao i u jednom trenutku upitao profesora:" Da li je Arhimed vaš prijatelj kada tako lepo govorite o njemu?"
Da su grčki matematičari i naučnici sledili Arhimeda umesto Euklida, Platona i Aristotela, oni bi, za dve hiljade godina, prestigli rezultate moderne matematike koja je počela s Dekartom i Njutnom u 17. veku, i moderene fizike koju je započeo Galilej u istom veku. |
Borka Marinković
Kompletni tekstove sa slikama i prilozima potražite u magazinu
"PLANETA" - štampano izdanje ili u ON LINE prodaji Elektronskog izdanja
"Novinarnica"
|

