MATEMATIKA
Borka Marinković
Nizovi
Beskonačno mnogo prostih brojeva
Većina testova sadrži geometrijske probleme (sposobnost apstraktnog mi- šljenja), a mnogi razne numeručke zadatke, od kojih je najviše tipa: nastavi niz...(logičko zaključivanje). Nastaviti niz znači: pronaći pravilo(a) po kojem se ređaju brojevi (članovi niza). Pravilo se sastoji od jedne ili više računskih operacija primenjenih na jednom broju da bi se izračunao sledeći. U složenijim zadacima može se kombinovati i više pravila.
Primeri:
1, 5, 9,11…(15,19…), lako se utvrđuje pravilo: +4 30, 25, 21, 18…(16, 15…) pravilo u ovom primeru je:- 5, –4, –3, –2… 1, 2, 0,3, –1…(4, –2...) pravilo je: +1, –2, +3, –4… 3, 5, 9, 17…(33, 65…) pravilo:x2 –1 1, 2,2, 3, 4,4,8... (5, 16...) kod ovog primera treba naglasiti da se moraju navesti 2 broja, iz čega se zaključuje da su primenjena dva različita pravila:+1 za prvi, treći, peti itd broj, i x2 za drugi, četvrti, šesti itd.
Na osnovu navedenih primera mogu se uočiti osnovne osobine matematičkih nizova. Niz (an) se sastoji iz članova (realni brojevi) poređanih po zadatom pravilu. Primenjujući ga, svaki član niza se mora nalaziti na tačno određenom mestu (redni broj člana) koji se naziva indeks člana i piše se: a1, a2 , a3... an,...an se naziva: opšti član. Brojni niz je preslikavanje ( funkcija) pri kojem se svakom prirodnom broju dodeljuje neki realan broj - a(n):NR U matematici, pravilo je moguće zadati na više na- čina: nabrajanjem, opisno… ali se najčešće zadaje navo- đenjem funkcije (pravila), tj. opšteg člana an. Npr. an = 2x n+1, nN ili rekurzivnom formulom, tj. vezom izme- đu dva uzastopna člana niza npr. an+1=an+d (aritmetički niz) Nizovi mogu biti sa konačnim brojem članova ilibeskonačni. Specijalni nizovi koji imaju veliku primenu su aritmetički i geometrijski niz.
Granična vrednost niza
Jedan od najvećih problema beskonačnih nizova je granična vrednost. Zapravo, šta se dešava sa opštim članom niza kada n neograničeno raste? U nizu a(n):1, ½,1/3,1/4...1/n... lako se uočava da se vrednost članova sve više smanjuje što je n veće, približavajući se broju 0, ali nikada neće biti jednaka 0. Zbog toga se kaže da je 0 granična vrednost (limes) niza. Geometrijsko objašnjenje ove činjenice je prihvatljivije za razumevanje. Ako se brojeve 1, 1/2, 1/3, 1/4, 1/5… prikažu na brojnoj pravoj i uoči neki interval oko broja 0, primećuje se da se konačno mnogo brojeva nalazi izvan tog intervala, dok će svi ostali članovi niza (njih beskonačno mnogo) upasti u zadati (ma koliko mali) interval.
Može se to iskazati i rečima:ako svi članovi nekog niza, osim možda njih konačno mnogo, imaju neku osobinu, onda se kaže da skoro svi članovi tog niza imaju tu osobinu. Ako niz ima graničnu vrednost, onda se kaže da je konvergentan. Ukoliko takav broj ne postoji, onda je niz divergentan. Gaus je 1813. strogim definicijama, prvi put u istoriji matematike, odredio uslove konvergencije nizova u graničnim uslovima. Savremenu definiciju limesa dao je češki matematičar Bernard Bolcano (1781-1848) u tada jedva primećenom radu: “Der binomsche Lehrsatz”, što je, posle više od pedeset godina, prihvatio nemački matematičar Vajerštras

Matematička indukcija
U prirodnim naukama se, prilikom posmatranja neke pojave ili vršenja eksperimenata, primenjuje metod zaključivanja kojim se iz stavova koji se odnose na određen (ograničen) broj pojedinačnih slučajeva iste vrste izvodi jedan opšti stav, tj. stav koji se odnosi na sve slučajeve iste vrste. Takav metod naziva se empirijska ili nepotpuna indukcija. Primenom ove metode dolazi se i do istinitih i do neistinitih zaključaka. Uprkos tome, njena uloga je značajna. Iako je matematika više deduktivna nauka, stvaralački i istraživački postupci u matematici su, po pravilu, induktivni. Najraniji tragovi matematičke indukcije mogu se naći u Euklidovom dokazu da postoji beskonačno mnogo prostih brojeva. Forma dokaza matematičkom indukcijom nalazi se u knjizi koju je napisao AlKaradži, oko 1000. godine. Ni jedan od njih nije eksplicitno dao induktivnu hipotezu. Prvi koji je strogo koristio ovaj metod, nameravajući da dokaže da je zbir prvih n neparnih brojeva jednak n2 bio je Frančesko Mauroliko u svom delu „Arithmeticorum libri duo” (1575. godine).
Indukciju su, takođe nezavisno, otkrili Švajcarac Jakob Bernuli i Francuzi Paskal i Ferma. Matematička indukcija je primer najsigurnijeg logičkog zaključivanja jer se mnogi stavovi strogo dokazuju, pa se koristi za dokazivanje u skoro svim oblastima matematike, naročito u nizovima. Princip matematičke indukcije se odnosi na rad sa prirodnim brojevima. Opisno:prvo se dokaže da je neki iskaz tačan za početnu vrednost P(1), a zatim se doka- že da je proces prelaska sa neke vrednosti na sledeću ispravan. P(n) P(n+1) Ako su oba tvrđenja dokazana, onda se do tačnosti iskaza za svaku vrednost može doći uzastopnim ponavljanjem ovog procesa. Ilustrativan primer je tzv. „domino efekat”.
Prva domina može da padne
Bilo koja domina da padne oboriće sledeću dominu pa se zaključuje da će se obaranjem prve domine, oboriti i sve domine koje se nalaze iza nje u nizu. 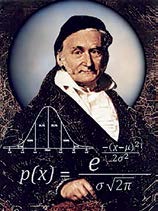
Primena nizova u programiranju
Učenicima je često teško da prepoznaju nizove na časovima informatike, tj. one koje su već obrađivali u matematici. U mnogim oblastima primene računara javljaju se skupovi podataka. Da se ne bi posebno imenovao svaki podatak, skupu podataka se dodeljuje zajedničko ime, a elementima skupa indeksi. U računarstvu, niz je skup podataka sa zajedničkim imenom. Svi članovi niza moraju da budu iste vrste (brojni, tekstualni, logički itd.) i iste dužine. U radu sa nizovima ne može se tretirati ceo niz već isključivo pojedinač- ni članovi. Svaki član niza se javlja kao tekuća vrednost posebne promenljive koja se zove indeksna promenljiva (brojač). Prema broju indeksa niza (1,2...), nizove delimo na jednodimenzionalne, dvodimenzialne (u matematici se zovu matrice) i višedimenzionalne. Pri opisivanju nizova s kojima će se raditi, mora se navesti (predvideti) ukupan broj članova svakog niza (dimenzija niza). Primer zadataka sa jednodimenzionalnim nizovima Svakog dana u toku jedne nedelje (meseca, godine…) potroši se izvesna suma novca.
Napisati program kojim će se u zadatom periodu: Izračunati ukupna potrošnja novca Prosečna potrošnja Odrediti najveća i najmanja potrošnja Odrediti dan u kojem je bila najveća i najmanja potrošnja Odrediti broj dana u kojima je potrošnja bila manja (veća) od prosečne, itd. Opisno rešenje zadatka: Ideja rešenja zadatka je dase uvede niz P (potrošnja) čiji članovi (x) predstavljaju potrošenu sumu svakog dana. Dimenzija niza je broj dana za koji se rešava zadatak. P(xi), i=1,ukupan broj dana. Indeksnom promenljivom se prolazi kroz sve članove niza i vrši sabiranje u posebnoj promenljivoj npr. S.
Za prosečnu potrošnju se izračunava vrednost S koja se podeli sa brojem dana za koji se računa. Određivanje max niza se vrši postupkom u kojem se pretpostavi ( uvede nova promenljiva max) da je tra- žena vrednost bila već prvog dana, pa se redom ispituje za svaki sledeći dan da li je ona veća od pretpostavljene. Ukoliko jeste, onda joj se dodeljuje nova vrednost i tako redom, do poslednjeg člana niza. Na kraju, sadržaj promenljive max je stvarno najveća vrednost. Postupak za najmanju je potpuno isti, jedino se postavlja pitanje: da li je nova vrednost manja od pretpostavljenog min? Odrediti dan kada je potrošnja bila najveća ili najmanja zahteva uvođenje promenljive koja čuva indeks (redni broj dana) kada je izvršena zamena, tako da će na kraju njena vrednost biti redni broj poslednjeg dana kada je izvršena zamena. Vrlo slično se rešava i poslednji problem u ovom primeru, u kojem se upoređuje vrednost svakog člana niza sa prosečnom vrednošću potrošnje i povećava vrednost promenljive (koja broji dane) za 1 svaki put kada je zadovoljen traženi uslov.
Excel kao dvodimenzionalni niz
Svima vrlo poznata primena niza je tzv. sortiranje niza, ređanje članova niza u rastućem (opadajućem) poretku. Osim u brojnim nizovima, sortiranje je vrlo prisutno u kod azbučnih (alfanumeričkih) nizova, kada se neka lista (niz) imena ređa po azbučnom redu. Ovi školski primeri pokazuju mogućnosti primene nizova. Dvodimenzionalni nizovi (članovi niza su određeni sa dva indeksa: broj reda i broj kolone) su tako- đe našli izuzetnu primenu u programiranju, pogotovu složenijih problema. Microsoft-ov program Excel (rad sa tabelama) je zapravo dvodimenzionalni niz. Korišćenje ovog izuzetno bogatog programa prilagođeno je korisnicima koji se ne bave profesionalno programiranjem. Planiranje, priprema proizvodnje pa i kompletno vođenje preduzeća, razne kvantitativne analize u istraživanjima, obrade podataka… prilično su pojednostavljene tako da se brzo dolazi do potrebnih rešenja. 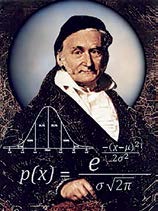
Borka Marinković
Kompletni tekstove sa slikama i prilozima potražite u magazinu
"PLANETA" - štampano izdanje ili u ON LINE prodaji Elektronskog izdanja
"Novinarnica"
|

