MATEMATIKA

Pripremila: Borka Marinković

Karl Fridrih Gaus

Vladar matemati čara

"Doterivanje i razvitak sistemske aritmetike, kao i sve drugo što je matematika 19. veka dala u smislu originalnih naučnih ideja povezano je s Gausom", rekao je veliki matematičar Leopold Kroneker. Gaus, vladar matematičara, u istoj klasi je sa Arhimedom i Njutnom. Povod za naredne redove je 160 godina od njegove smrti.

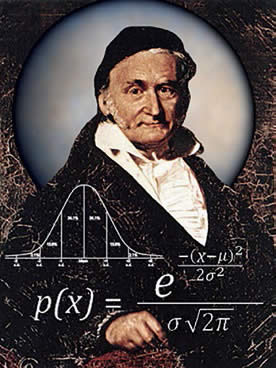Iako je živeo 78 godina, ovaj univerzalni i plodan naučnik se samo matematikom bavio do svoje 25 godine. A počeo je veoma rano. Sa manje od tri godine uočio je grešku u računu svog oca, neobrazovanog čoveka koga je plašilo sve u vezi sa naukom. Zahvaljujući svom mudrom ujaku, pošao je u školu. Čudo od deteta, mali Karl zadivio je svog učitelja Bitnera rešivši izuzetno težak zadatak za minut. Trebalo je izračunati zbir 81297+81495+...+100899, koji predstavlja aritmetičku progresiju od 100 članova sa razlikom 198. Zahvaljujući izuzetnom talentu, Gaus je dobio svog prvog značajnog prijatelja u učitelju.

Bitner mu je odao priznanje, nagradio ga matematičkim knjigama i uputio ga na podučavanje perspektivnom asistentu Martinu Bartlesu, koji je kasnije postao profesor matematike u Rusiji. Sedamnaestogodišnjem Bartlesu bilo je jasno šta se krije u čudesnom mozgu njegovog desetogodišnjeg prijatelja. Zajedno su učili, pomagali jedan drugom u savlađivanju teškoća i pisanju radova. Već na osnovu prvog rada, mladi Gaus je shvatio da matematika treba da teži krajnjoj preciznosti, jer tačan rezultat ne znači neminovno i tačan postupak koji je doveo do njega. Time je krenuo novim matematičkim putevima, koji su se bitno razlikovali od svih puteva velikih analitičara svog vremena: Njutna, Lagranža, Laplasa, Ojlera, omogućivši svojim naslednicima Abelu, Košiju, Vajerštrasu i drugima da dovrše veličanstvenu građevinu algebre.

Doživotni mecena i prijatelj

Bartles je uveo Gausa u tajne aritmetike i na vreme preduzeo sve da mu osigura bogatog mecenu. Vojvoda od Braunšvajga Karl Vilhelm Ferdinand primio je Gausa 1791. Njegova skromnost, nespretna plašljivost, ali pre svega genijalnost su ga očarale. Zahvaljujući vojvodinoj finansijskoj pomoći, sledeće godine, sa svojih petnaest godina, Gaus je nastavio školovanje na Karolinskom koledžu. Karl je pre upisa na koledž završio dvogodišnji kurs klasičnh jezika: latinskog i grčkog. U njemu se krio nesuđeni filolog a ljubav prema jezicima iskazao je napisavši svoje najveće radove na latinskom. Impozantna je činjenica da je u šezdesetoj godini naučio ruski tako da je čitao ruske klasike u originalu; na tom jeziku je mogao da vodi i konverzaciju.

Gaus je na koledžu studirao tri godine i za to vreme dao mnoge radove iz svoje omiljene oblasti - aritmetike, zbog kojih je postao besmrtan. Proučavajući prethodnike, najviše se bavio Njutnom, nazivajući ga summus , dok su svi ostali dobili kompliment clarissimus . Najznačajni rad iz tog perioda poznat je kao „zakon kvadratnog reciprociteta“.

Prekretnica

Interesantno je da devetnaestogodišnji Gaus, iako već uspešan matematičar, još nije odlučio da li će se baviti tom naukom ili filologijom. Prelomni datum bio je 30. mart 1796. Tog dana rešio je problem konstrukcije pravilnog sedamnaestougla (heptadekagona), koristeći rešenja binomne jednačine x 17 =1. O duševljen tim otkrićem, odlučio se za matematiku. Ponosan, izrazio je želju da ovaj pravilni poligon bude ugraviran na njegovom nadgrobnom spomeniku.

Njegova želja nije ostvarena jer je kamenorezac smatrao da se mnogougao sa sedamnaest jednakih stranica ne bi razlikovao od kruga. Međutim, na spomeniku u Braunšvajgu je ipak izgraviran "njegov" poligon.

Gausov matematički dnevnik

Ovaj datum je i za Gausa i za razvoj matematike značajan po tome što je Gaus tog dana počeo da vodi svoj naučni dnevnik (Notizenjournal) u koji je unosio beleške do 1814. To je jedan od najdragocenijih dokumenata u istoriji matematike. Na prvoj stranici zapisao je svoju upravo rešenu konstrukciju.

Dnevnik se nalazio kod Gausovog unuka pune 43 godine posle matematičareve smrti. Godine 1901. objavio ga je nemački matematičar Feliks Klajn, pošto ga je Kraljevsko društvo u Getingenu pozajmilo radi proučavanja. Ovo neveliko delo sadrži 146 neobično sažetih beleški od kojih svaka predstavlja jedno poglavlje u matematici.Beleške su primer kondenzovanosti matematičkog mišljenja i nije ih bilo lako protumačiti. Jedna od najneobičnijih izgleda ovako:

?YPHKA! num =?+?+?

Reč ?YPHKA najviše podseća na Arhimedov trijumfalni uzvik "Eureka" (Pronašao sam!) Matematičko objašnjenje je da je svaki prirodni broj zbir najviše 3 trougaona broja ( 0,1,3,6,10...) ( n(n+1)/2)

Savremenici su molili Gausa da ublaži svoju krutu savršenost, ali se on nije obazirao na njihove molbe. Ideal mu je bila gotska katedrala koja tek posle sklanjanja skele deluje svojom veličanstvenom arhitekturom. Delo mora biti zrelo i do kraja ostvareno da bi se objavilo svetu. Panca sed matura ( Malo, ali zrelih)

Zašto Gaus nije objavljivao svoja otkrića? Ima više pretpostavki, između ostalih da mu je Akademija odbila štampanje remek-dela "Aritmetička istraživanja" ("Disquisitiones") što nikada nije potvrđeno. Pre svega, radi se o njegovoj skromnoj prirodi i posvećenosti radu. Na žalost, pri tome nije razmišljao da bi njegovi veliki rezultati mogli pomoći naslednicima. Abel i Jakobi nisu nastavili tamo gde je Gaus stao već su uložili najveće napore da ponovo otkriju ono što je Gaus znao pre nego što su oni bili rođeni. Takođe, stvarala se i konfuzija ko je autor nekih značajnih rezultata.

Getingen i "Disquisitiones"

Tri godine boravka na Univerzitetu u Getingenu bile su najplodonosnije u Gausovom životu. Zahvaljujući plemenitosti vojvode Ferdinanda, mladi naučnik nije imao finansijskih problema pa se potpuno posvetio matematici. 1798. odbranio je doktorsku disertaciju u kojoj je dao prvi strogi dokaz osnovnog stava algebre, kojim se tvrdi da proizvoljni algebarski polinom n-tog stepena ima tačno n rešenja i završio veliki rad na teoriji brojeva uobličen u "Disquisitiones", majstorskom delu, koga mnogi smatraju najvećim. Na taj način se, sa svoje 24 godine, oprostio sa "čistom" matematikom kao jedinom naučnom oblasti proučavanja. Knjiga je objavljena tri godine kasnije, s posvetom dobrotvoru Ferdinandu: "Vaša plemenitost oslobodila me je svih drugih briga i omogućila mi da se tome potpuno posvetim".

Bez sumnje, Gaus je mogao dobiti mesto profesora matematike, ali on je više voleo opservatoriju, koja mu je pružala bolje mogućnosti za naučni rad. Drugi razlog je što ga nije privlačila profesura, pogotovu prosečnim studentima.

Skoro četrdeset godina proveo je radeći kao direktor opservatorije u Getingenu. U poslednjuh dvadeset, samo je jednom napustio Getingen da bi video gradnju železničke pruge, jer ga je uvek privlačilo sve u vezi železnice. "Čovek ne mora uvek leteti iznad globusa da bi video šta se događa. Mozak i sposobnost čitanja novina (čak i kad one lažu) i vladinih izveštaja (naročito kad i oni lažu) katkada su bolji od bilo kog razgledanja grada i brbljanja u hotelima."

Pojmova koje nose Gausovo ime

Gaus je tvorac aritmetike kompleksnih brojeva, koju je razvio 1831. Postavio je kompleksne brojeve ( a+ib, a,b Î R) kao tačke u ravni.

Rimanova hipoteza o osnovama geometrije uopštavanjem prostora je bila toliko ispred svog vremena da je jedino Gaus mogao shvatiti njenu dubinu.

Napisao je pionirsku studiju o hipergeometrijskim redovima, zahvaljujući čemu su Abel i Koši izradili sistemsku primenu beskonačnih redova i zasnovali teoriju konvergencije.

Simboli u matematici koje je uveo Gaus: o kongruencija, O proizvod.

Gausova kriva (kriva zakona normalne raspodele), Gausova (Zajdelova) metoda rešavanja sistema linearnih jednačina.

Anštajn je bio najmiliji Gausov učenik. Takođe, njegovi studenti su veliki matematičari Dedekind i Riman.

Univerzalni Gaus

Iako je bio matematički "princ", Gaus nije nikada apsolutizovao matematiku, za razliku od mnogo manjih od njega. Pisao je da postoje problemi čije je rešavanje za čovečanstvo mnogo značajnije od čisto matematičkih, kao npr. "oni koji se tiču etike ili našeg odnosa prema bogu, ili se tiču naše sudbine i naše budućnosti, ali njihovo rešenje leži potpuno izvan nas i potpuno izvan područja nauke". Univerzalni naučnik u punom smislu te reči Gaus je ostavio rezultate u mnogim oblastima kojima se bavio: elektromagnetizmu (brod koji poseduje zaštitu od magnetnih mina, u pomorskoj terminologiji zove se "degausovan"), elektrostatici, u izradi električnog telegrafa koji je koristio u komunikaciji sa prijateljem Veberom, optici, astronomiji, geodeziji (otkrio heliograf), nebeskoj mehanici. Izračunao je 1801, na osnovu oskudnih podataka, celokupnu putanju asteroida Ceresa, što mu je u to vreme donelo veću popularnost od svega što je do tada uradio u matematici. Po njemu su nazvani Gausov zakon magnetizma, Gaus-Krigerov koordinatni sistem, Gausov integral.

Džepni sat je zauvek stao

Gaus je bio impresioniran matematičkim sposobnostima francuske matematičarke Sofi Žermen, iako je nikada nije video. Ona je vodila prepisku sa Gausom pod muškim pseudonimom, obzirom na tadašnju diskriminaciju žena, pogotovu u nauci tako da je on slučajno otkrio njen identitet. Njegovim zauzimanjem, ona je od Getingenskog univerziteta dobila titulu počasnog doktora.

Gaus je iz dva braka imao šestoro dece. Osim jednog sina, niko nije nasledio raskošan očev talenat.

Nikada se nije žalio na zdravlje, iako mu se narušavalo. Samo jednom, zabelezio je u svom dnevniku, iznenada, između redova o eliptičkim funkcijama rečenicu: "Smrt mi beše milija od života." Ovim rečima ga je opisao prijatelj Sartorino : "Kakav beše u mladosti, takav je ostao i u starosti do poslednjih dana, nepromenjen, jednostavan..."

Gaus je preminuo 23. februara 1855. u 1:05 ujutro. Njegov džepni sat, koji se nosio sa sobom skoro celog života, prestao je da kuca skoro u isto vreme.

Borka Marinković

Kompletni tekstove sa slikama i prilozima potražite u magazinu
"PLANETA" - štampano izdanje ili u ON LINE prodaji Elektronskog izdanja
"Novinarnica"