TEMA BROJA - Šah između igre i uma
Pripremila: Borka Marinković
Matematika
Nemoćni car ispred 64 polja
Pretpostavlja se da je šah izmišljen u Indiji. Prvo se zvao "čaturanga" po indijskoj reči koja znači "sastavljen iz četiri dela" po rodovima indijske vojske: borna kola, slonovi, konjica i pešaci. Igrala su ga četiri igrača. Tokom nekoliko vekova se raširio po Srednjoj Aziji. Promenila su se pravila igre pa su ga igrala dva igrača. Pri kraju srednjeg veka postao je poznat i Evropljanima koji su mu dali novo ime "šahmat" po persijskoj reči "šah" (kralj) i arapskoj "mat" (mrtav).
O ovoj drevnoj i stolećima dugoj igri postoje mnoge legende. Jedna od najpoznatijih je sledeća...
 Indijski car Šarem bio je poznat po surovosti prema potčinjenima. Naučnik po imenu Seta je izmislio "čaturangu", smatrajući da će pomoću nje promeniti carevo ponašanje. Ideja se sastojala u tome da kralj , iako glavna figura, ne može opstati bez odbrane i pomoći svojih saboraca - ostalih figura.
Kada je car naučio ovu igru, oduševljen njenim kvalitetom, odlučio je da nagradi tvorca. Obratio se Seti: "Želim da te dostojno nagradim za prekrasnu igru koju si pronašao. Dovoljno sam bogat i mogu ispuniti svaku tvoju želju. Kaži koju bi nagradu najviše voleo i dobićeš je". Seta se zahvalio caru na dobroti i zamolio ga da mu ostavi vremena da razmisli.
Sledećeg dana je iznenadio cara skromnom željom: "Gospodaru, naredite da mi se za prvo šahovsko polje da jedno pšenično zrno, za drugo dva, za treće četiri, tj. za svako sledeće duplo više nego za prethodno i tako za sva polja".
"Dosta", ljutito ga je prekinuo car, "dobićeš zrna za sva šezdeset četiri polja šahovske table, prema svojoj želji. Ali znaj, tvoja želja nije dostojna moje darežljivosti. Tražeći tako malu nagradu, omalovažavaš moju milost. Odlazi! Moje sluge doneće ti tvoju vreću pšenice".
Seta se osmehnuo i otišao u carski vrt da sačeka nagradu. Dvorskim matematičarima bila su potrebna dva dana da izračunaju koliko zrna pšenice treba da dobije Seta. To je veoma razljutilo cara koji nije shvatio o koliko velikom broju zrna se radi.
" Koliko velik bio da bio", nadmeno im se obratio car,"moje žitnice ne oskudevaju. Nagrada je obećana i treba da se preda Seti".
"Nije u vašoj moći, gospodaru, da isporučite obećanu nagradu. U svim vašim ambarima nema toliko zrna pšenice koliko treba isporučiti Seti. Ako želite da ispunite obećanje, naredite da se sva zemaljska prostranstva pretvore u oranice, isuše sva mora i okeani, istopi sav led i sve to zaseje pšenicom. Sav taj rod treba predati Seti".
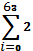(  i =2+2 2 +2 3 +2 4 +....2 63 = 18 446 744 073 709 551 615)
Izračunavanje rejtinga šahista
Reč rejting potiče od engleske reči rating koja znači: ocena.
Prvi pokušaj uvođenja sistema vrednovanja šahista bio je početkom 20. veka, a krajem pedesetih godina prošlog veka počela je praktična primena nekoliko sistema. Oni su se zasnivali na tome da se svakom šahisti dodeljuje individualni koeficijent, izračunat po određenoj formuli, koji zavisi od koeficijenta protivnika i pokazanog rezultata. Ako šahista prvi put učestvuje na turniru na kome se primenjuje dati sistem, on dobija početni koeficijent K o. Dalje, posle svakog takmičenja, koeficijent se izračunava tako što se pre svega utvrđuje očekivani broj bodova koji šahista mora skupiti da bi sačuvao svoj stari koeficijent (do početka turnira). "Novi" koeficijent K nov (posle završetka turnira) izračunava se po formuli
K nov = K st +? ( N-N oč ), gde je N - broj osvojenih bodova, a ? - "vrednost" jednog boda u sistemu. (U nekim sistemima formula ima složeniji oblik). Ako je N>N oč , onda rejting raste, a ako je N<N oč "rejting" opada.
 |
Živi šah u Mariboru |
Tačno je da sistem individualnih koeficijenata ne odražava stvaralačku snagu šahista već uzima u obzir samo sportske uspehe. Međutim, praksa je pokazala da su rezultati šahiste i njegova stvaralačka dostignuća, po pravilu, u tesnoj vezi.
Kada su šahisti, između više sistema, prihvatili matematički prilaz oceni svojih rezultata, 1970, Međunarodna šahovska federacija (FIDE) prihvatila je sistem profesora matematike A. Elo-a koji je zasnovan na individualnim koeficijentima. Svoje službene rejting-liste FIDE objavljuje dva puta godišnje.
U okviru svog sistema Elo je izračunao koeficijente svih najvećih šahista od vremena Morfija. Godine 1963. objavio je listu u kojoj je je za svakog velikog šahistu izračunao rejting na osnovu rezultata u periodu od njegovih najboljih pet godina. Spisak sadrži 28 imena čiji su rejtinzi veći od 2600 (Lasker, Kapablanka, Botvinik 2720, Talj 2700, Morfi 2690, Aljehin, Smislov 2680, Rubinštajn, Eve, Gligorić 2640...)
Prvi zvanični meč za titulu svetskog prvaka u šahu odigran je 1886, u tri američka grada (Njujork, Sent Luis, Nju Orleans) između Vilhelma Štajnica i Johanesa Cukertorta. Štajnic je pobedio rezultatom 10:5, uz 5 remija, i tako postao prvi zvanični prvak sveta.
Primeri matematičkih zadataka sa temom iz šaha
• Četiri igrača su igrala šah. Svaki igrač je odigrao po jednu partiju sa ostalima. Koliko partija je odigrao svaki igrač?(3) Koliko je ukupno partija odigrano? Odgovor: 3 i 6
 |
Anatolij Karpov |
• Na jednom šahovskom turniru na kome je svaki šahista odigrao po jednu partiju sa ostalima, odigrana je ukupno 231 partija. Koliko šahista je učestvovalo na ovom turniru? Odgovor: 22 igrača
• Na šahovskom turniru jedan igrač odigrao je 12 partija. Kada su ga pitali koliko je partija dobio, odgovorio je: "Dve partije sam izgubio, a od ostalih na svake dve nerešene, ja imam tri pobede." Koliko ovaj takmičar ima pobeda ? Odgovor: 6
• Na jednom šahovskom turniru učestvovala su dva učenika 7. i izvestan broj učenika 8. razreda. Svako je igrao sa svakim po jednu partiju. Dva učenika 7. razreda osvojila su ukupno 8 poena, a svi učenici 8. razreda sakupili su podjednak broj poena. Koliko je "osmaka" učestvovalo na turniru? (poraz - 0 poena, nerešeno - 1 poena, pobeda - 1 poen). Odgovor: 7 i 14. (Zadatak je sa IX Ruske matematičke olimpijade, 1946)
• Da li je moguće sva slobodna polja šahovske table 5x5 polja pokriti pločicama domina odgovarajućih dimenzija ( svaka pokriva dva susedna polja)? Odgovor: nije
• Na praznu šahovsku tablu treba postaviti dva pešaka različite boje. Koliko različitih položaja oni mogu zauzeti na ovakvoj tabli? Odgovor: 4032
• Sa koliko najmanje poteza lovac može sa polja h1 doći na polje a8 prolazeći samo kroz sva bela polja? Odgovor: 17
• Ako se skakač, polazeći sa jednog polja, kreće kao u šahu i ako slova sa polja na koja je skočio ređamo jedno za drugim (sve dok ne obiđu sva polja, ali ni jedno polje dva puta) dobiće se ime čuvenog grčkog matematičara.
• Može li skakač, pomerajući se po šahovskoj tabli po pravilu skakača počevši od polja a1, da stigne na polje h8 a da se pri tom nađe na svakom polju tsamo jedanput? Odgovor: ne može. (Zadatak sa Opštinskog takmičenja iz matematike učenika II razreda srednje škole, održanog 1980)
• Na koliko se različitih načina može postaviti jedan beli i jedan crni top tako da se ne napadaju? Odgovor: 896
• Kako na šahovsku tablu postaviti četiri dame i jednog pešaka tako da sva polja budu zauzeta ili napadnuta? Odgovor: dame na poljima c2, d6, g1 i h5, a pešak na polju b7
Anatolij Karpov: šta je zajedničko?
- Matematika i šah imaju mnogo zajedničkog. U matematici je najvažnije logički misliti tj. "raditi glavom", a tako je i u šahu.
Nije slučajno što se šahovske i matematičke sposobnosti često dovode u vezu. Neki raniji šampioni sveta u šahu su bili i poznati matematičari (Štajnic,Lasker, Eve), dok su neki znameniti matematičari prema šahu ispoljili određeni naučni interes
(Gaus, Ojler). Šahovska tabla i figure, pa i sama igra, često se koriste kao ilustracija za razne matematičke zadatke.
Da bi se postigao uspeh u matematici, potrebno je nešto sposobnosti i mnogo više rada i vežbanja, smatra Karpov.
Borka Marinković
Kompletni tekstove sa slikama i prilozima potražite u magazinu
"PLANETA" - štampano izdanje ili u ON LINE prodaji Elektronskog izdanja
"Novinarnica"
|
