FIZIKA
Pripremio: D. Čevizović
Solitoni
Nerazrušivi talasi Za talase znamo od pamtiveka. Najverovatnije su prvo opaženi na površini vode. Solitoni su međutim primećeni tek u 19. veku. Od tada je ovakav vid talasnog kretanja prepoznavan na sasvim neočekivanim mestima: od beskrajnih prostranstava vasione do molekularnog nivoa, čak i dublje, u strukturi samog prostora i elementarnih čestica!
 Talasi su vid kretanja materijalne sredine pri kojem njeni delići osciluju oko svojih ravnotežnih položaja, a sa susednim delićima povezani su elastičnim silama. Usled postojanja ovakvih sila, oscilovanje prvobitno pobuđenog delića se prenosi na njegove susede i nastaje (elastični) talas. Neke bitne osobine su: ako nekoliko talasa različitih frekvencija i (ili) amplituda složimo, nastaje novi talas, koji može imati sasvim drugačiji oblik od talasa koji su učestvovali u njegovom slaganju. Ovakvim sabiranjem mogu nastati talasne formacije u obliku velikog brega (obično praćenog nizom bregova mnogo manjih amplituda), tzv. „ talasni impuls “. Kretanjem talasnog impulsa prenosi se energija. Iako podseća na „cunami“, talasni impuls koji je nastao slaganjem “linearnih“ talasa ne može opisati ovakvo kretanje vodene mase. Razlog tome je disperzija „linearnih“ talasa: talasni impulsi nastali njihovim slaganjem se veoma brzo rasturaju ili, kako bi rekli fizičari, njegovo „vreme života“ je nedovoljno da bi prešao neko veće rastojanje i sa sobom preneo rušilačku energiju.
Veliki ujedinjeni talas
U avgustu 1834. škotski inženjer Džon Skot Rasel pratio je kretanje barže koju su po uskom kanalu vukli konji. U jednom trenutku barža se zaustavila ali je masa vode koju je ona gurala ispred sebe nastavila da se kreće: veća masa vode se nakupila ispred nosa plovila i odjednom velikom brzinom krenula napred, ostavljajući baržu daleko iza sebe. Okrugao, gladak i jasno izražen vodeni breg je produžio da se kreće po kanalu bez vidne promene oblika ili smanjenja brzine. Rasel je pratio kretanje čudnog talasa koji je tek nakon nekoliko kilometara počeo da gubi oblik. Bio je toliko iznenađen ovim otkrićem da je odmah počeo da ga proučava i nazvao ga je translatorni talas .
U to vreme su osnovni principi hidrodinamike bili jasno formulisani i prevedeni na jezik matematike. Ovaj posao su 1755. godine obavili Leonard Ojler (1707-1783) i 1823. godine Klod Luj Navije (1785-1836). Rasel se zato nije ograničio na puko opisivanje translatornih talasa. Usledili su brojni eksperimenti na vodi u kojima je između ostalog merio i njihove brzine (merenja su vršena u zalivu Fert-of-Fort i na reci Di v Češir). Sumirajući dobijena zapažanja, Rasel je ustanovio sledeća svojstva translatornih talasa:
1. brzina i oblik translatornog talasa se ne menja
2. brzina zavisi od visine talasnog brega i dubine kanala (pri tome visina brega mora biti manja od dubine kanala)
3. dovoljno velik talas se raspada na dva (ili više) talasa po sledećoj šemi: talas se „oslobađa“ suvišne mase i ostavlja je iza sebe. Odeljeni talas se kreće sporije od „roditeljskog“ talasa
4. kada se dva velika translatorna talasa susretnu, oni prolaze jedan kroz drugi, bez promene oblika ili brzine .
Osim toga, klasifikovao je pokrete vodene mase na četiri vrste kao i na dva tipa talasa: ujedinjeni i grupni. U grupne talase je ubrajao kapilarne talase i talase na površini vode, a translatorne talase je kasnije nazvao „ velikim ujedinjenim talasom “. Pojam ujedinjenog talasa je preživeo do današnjih dana i pod njim se podrazumeva svaki (najčešće zvonast) ravan talasni impuls, koji se premešta u nekom smeru i pri tome održava svoj oblik.
Godina 1834.
Otkrića koja su se desila 1834. godine i danas utiču na nauku. Te godine je irski matematičar Viljem Rouan Hamilton jednačine klasične mehanike formulisao u kanonskom obliku i otkrio optičko-mehaničku analogiju. Ovo je odigralo važnu ulogu u postavljanju teorijskih osnova kvantne mehanike. Iste godine je Klapeiron naučnoj javnosti predstavio rad Sadia Karnoa, koji je suštinski uticao na razvoj termodinamike. Majkl Faradej je te godine otkrio zakone elektrolize i predvideo postojanje elementarnog naelektrisanja. Engleski matematičar Čarls Bebidž je ustanovio osnovne principe njegove „analitičke mašine“, što je uticalo na potonji razvoj računarskih mašina. Na kraju, u okolini Edinburga je te godine prvi put primećen soliton. |
Rasel je svoje rezultate publikovao 1844. godine. Oni su kasnije privukli pažnju mnogih fizičara, koji su pokušavali da ih analitički opišu. Interesantno je međutim da se Hamilton, iako je dobro poznavao fiziku talasa i bio blagonaklon prema Raselu, nije uključio u raspravu: u to vreme je bio okupiran svojim novim otkrićem, kvaternionima.
S druge strane, pojavilo se i mnogo kritičara koji su sumnjali u tačnost Raselovih zaključaka i u postojanje translatornih talasa. Među njima je bio i Džordž Gabrijel Stoks (1819-1903), čije jednačine danas poznaje svaki student kursa hidrodinamike. Tek su 1895. godine u radovima profesora Amsterdamskog univerziteta Johanesa Kortevega (1848-1941) i njegovog učenika Gustava de Friza (1866-1934) izvedene i rešene parcijalne diferencijalne jednačine koje mogu opisati Raselove talase. Ove jednačine danas poznajemo kao Korteveg - de Frizove (KdF) jednačine.
Šta je zajedničko Fermiju, Pasti, Ulamu, Menhetn projektu i solitonima?
|
| Vek kasnije, 1995. godine, na konferenciji koja se održala na Heriot-Vat univerzitetu, u Škotskoj i bila posvećena teoriji solitona, ponovljen je opit u kojem je pobuđen solitonski talas na vodi u kanalu Union. Učesnici konferencije su tada imali priliku da posmatraju talase kakve je prvi opazio Skot Rasel |
Čuveni nuklearni fizičar Enriko Fermi (1901-1954) je sredinom 50-tih godina napustio istraživanja vezana za nuklearni program SAD. Ipak, ostao je u vezi sa dvojicom svojih saradnika, Džonom Pastaom (1918-1984) i Stanislavom Ulamom (1909-1984) u laboratorijama Los Alamosa jer je tu imao pristup novoizgrađenoj računskoj mašini namenjenoj numeričkom rešavanju pojedinih problema. Mašinu je trebalo testirati i postaviti zadatak koji bi maksimalno opteretio njene resurse, pa je Fermi predložio da se isproba rešavanje problema koji je davno postavio Piter Debaj: da se objasni konačna toploprovodnost čvrstih tela. Za model su uzeli anharmonijski lanac u kojem su 32 kuglice zadane mase povezane oprugama. Pri razvlačenju, opruge su na mase delovale silom koja bi imala dve komponente: linearna Hukova (proporcionalna prvom stepenu dužine rasteznja opruge) i sila znatno manjeg intenziteta, ali koja je proporcionalna drugom stepenu rastezanja opruge.
Kada se u sistemu čestica povezanih elastičnim oprugama pobudi samo jedna moda oscilovanja (moda tačno određene frekvencije), energija koju predajemo pobuđivanjem se neograničeno dugo zadržava na ovoj modi (tj. ostale mode drugih frekvencija se ne pobuđuju: sistem sve vreme osciluje na isti način). Fermi je bio uveren da, ako se u sistemu pobudi najniža moda oscilovanja (moda sa najmanjom frekvencijom oscilovanja i najvećom talasnom dužinom), zbog prisustva male (po intenzitetu) nelinearne komponente interakcije, energija pobude će polagano prelaziti na više mode (i one će se postepeno pobuđivati). Proces preraspodele energije bi trebalo da traje sve dok se celokupna energija pobude ravnomerno raspodeli po svim harmonicima. Drugim rečima, Fermi je očekivao da se u sistemu uspostavi termodinamička ravnoteža ili, kako to vole da kažu fizičari, da dođe do termalizacije sistema. Ovakav ishod bi bio u saglasnosti sa ponašanjem određenih (u to vreme poznatih) nelinearnih sistema. Kao rezultat, sistem bi trebalo da osciluje na složen način, koji uopšte ne liči na sinusnu funkciju.
|
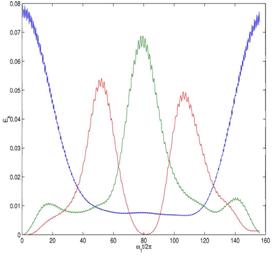
Promena ukupne energije (kinetička + potencijalna) oscilujućeg lanca u vremenu, za tri najniže normalne mode oscilovanja. Jasno se vidi da je u početku pobuđena samo osnovna moda k=1 (plava kriva). Druga i treća moda nisu pobuđene. Kako vreme protiče, pobuđuju se i ostale mode (druga, k=2, prikazana zelenom krivom, treća, k=3, prikazana crvenom krivom, i.t.d.). Na kraju, međutim, gotovo sva energija je ponovo lokalizovana na prvoj normalnoj modi! |
Proračuni koje je računar izvodio su u početku bili saglasni sa Fermijevim očekivanjima. Jednog dana je, međutim, računar ostavljen da proračune izvodi duže vreme. Kada su se vratili u računarsku sobu, Fermijeve saradnike je sačekalo iznenađenje. Nakon većeg broja perioda osnovne mode, gotovo sva pobudna energija se ponovo lokalizovala na ovoj modi! Sistem se uporno odupirao termalizaciji! Ovi neočekivani rezultati podstakli su dalja istraživanja nelinearnih sistema iz kojih su nastale dve savremene oblasti fizike: teorija solitona i teorija haosa.
Univerzalne pojave imaju osobinu da se neočekivano pojave u raznim oblastima ne samo fizike nego i drugih nauka. Solitoni su tako uskoro uočeni u fizici plazme. Rolad Zinurovič Sagdejev je 1957. godine razvijao teoriju udarnih talasa u plazmi. Ovakvi talasi se na primer stvaraju pri strujanju solarnog vetra oko Zemlje. Sagdejev je primetio da i ovde mogu nastati talasi slični onima koje je Rasel posmatrao na površini vode.
... i bi soliton ...
Fizikom plazme su se bavili i fizičari Martin Kruskal (1925-2006) i Norman Zabuski (1929-). Oni su zapazili da, ukoliko broj čestica u lancu Fermija, Paste i Ulama neograničeno raste, tada on postaje sličan (neprekidnoj) nelinearnoj struni, čija se mala oscilovanja opisuju... KdF jednačinom! Ovo znači da je odsustvo termalizacije energije u lancu povezano sa stabilnošću solitona koji se u njemu obrazovao. A soliton ne menja oblik za vreme svog rasprostiranja po lancu. Osim toga, Kruskal i Zabuski su proveli neke dodatne numeričke eksperimente i primetili da je sudar dva solitona veoma složena pojava, čiji ishod zavisi od brojnih fizičkih faktora. Kada se sudare dva lokalizovana talasna impulsa nastala slaganjem linearnih talasa, oni se u oblasti susreta slažu, a nakon toga nastavljaju da se kreću nezavisno jedan od drugog, kao da se nikada nisu sreli. Sa slaganjem solitonskih impulsa stvari stoje sasvim drugačije: u ovom slučaju matematičke procedure razvijene za opis linearnih talasa (zasnovane na primeni Furijeove analize) više ne funkcionišu.
Teorija solitonskih interakcija je posebna grana fizike talasa. U slučaju solitona koji predstavljaju rešenje KdF jednačine, ishod sudara dvaju solitona zavisi od odnosa njihovih brzina. Kada je odnos brzina veći od 3, dva solitonska impulsa se najpre spoje, a zatim razdvoje, zadržavajući prvobitni oblik i brzinu. Ovakvo ponašanje je, ako se prisetimo, u svojim eksperimentima primetio i Rasel jedan vek ranije. Ako je odnos brzina impulsa manji od 3, talasi prvo "odskoče", a zatim izmene i brzine i oblik. U oba slučaja može se zapaziti izvesna skokovita promena položaja i bržeg i sporijeg solitonskog impulsa. Na sreću, Kruskal i Zabuski se nisu ograničili samo na numeričke proračune: 1967. godine su otkrili način da dobiju tačna rešenja nelinearnih jednačina KdF tipa. Osim što su uspeli da objasne rezultate koje su dobili Fermi, Pasta i Ulam, Kruskal i Zabuski su u izvesnom smislu i kumovali ovoj interesantnoj pojavi. Oni su predložili naziv „ soliton “ i uveli ga u fiziku. Time su hteli da istaknu sličnost koju su otkrili između osobina solitona i čestica.
Ipak, rani pokušaji da se statistički objasni zašto se prelaz energije sa osnovnog na više harmonike ne dešava nisu uspeli. Prvi uspeh je postignut kada je na ovaj problem primenjen adaptirani metod usrednjavanja Bogoljubova i Krilova, u prvoj polovini 60-tih godina.
Kako nastaje soliton?
Pojam disperzije je u fiziku linearnih talasa uveo Isak Njutn. Pod ovim pojmom se podrazumeva zavisnost brzine prostiranja talasne faze od talasne dužine (ili frekvencije oscilovanja). Disperzija je uzrok rasturanja talasnih paketa, neravnomernog kretanja talasnog fronta i mnogih drugih pojava. Upravo zbog postojanja disperzije, Ervin Šredinger je odustao od modela "razmazanog elektrona" koji je predlagao Luj de Brolj, pošto bi grupa de Broljevih talasa koja formira talasni paket dimenzije elektrona trebalo da se rasturi za 10^-26 sekundi!
|
|
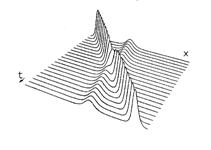
Sudar dvaju solitona. Levi grafik prikazuje rešenje KdV jednačine u xt ravni, za slučaj kada je viši (i brži) soliton u početnom trenutku (t=0) postavljen levo od nižeg. U jednom trenutku solitonski impulsi se sustignu i "sudare" (trenutak sudara je u centru crteža). Lako se zapaža da:
1) putanje solitonskih impulsa pre i posle sudara su malo pomerene: talasi "trpe" fazni pomak (bolje se vidi na talasu manje amplitude);
2) maksimum talasa u oblasti sudara je manji od maksimuma talasa veće amplitude (što ukazuje na odsustvo linearne superpozicije talasa);
3) talasi posle sudara zadržavaju pređašnji oblik. |
Brzina nelinearnih talasa zavisi ne samo od talasne dužine već i od njegove amplitude. Kada je nelinearnost u interakciji čestica koje grade sredinu kroz koju se talas prostire mala, talas može da se predstavi skupom harmonika koji se prostiru svaki svojom brzinom (disperzija). Usled postojanja nelinearnosti, oni među sobom interaguju. Ako je disperzija mala, energija pobude se preraspodeljuje sa bržih na sporije mode. Kada ovakva preraspodela energije uspeva da neutrališe rasturanje talasnog paketa zbog disperzije, rađa se stabilna formacija: soliton! Kraće rečeno, solitoni se formiraju kada se efekti disperzije talasne grupe fino izbalansiraju sa efektima koje uzrokuje nelinearnost u interakciji među česticama koje grade sredinu kroz koju se talasna grupa prostire. Ako jedna grupa efekata nadjača drugu, soliton nestaje!
Teorija solitona danas
Postoji velik broj nelinearnih parcijalnih diferencijalnih jednačina. Međutim, nemaju sve solitonska rešenja. Od važnijih primera jednačina sa solitonskim rešenjima već smo govorili o Korteveg de Frizovoj jednačini. Ona ima važnu ulogu u matematičkom opisu nelinearnih talasa u hidrodinamici: kao što smo rekli, ovom jednačinom su opisani Raselovi vodeni talasi. Osim toga, uspešno je opisan Fermi-Pasta-Ulamov problem u kontinualnom limitu. Danas se ova jednačina koristi za opis i nekih drugih pojava u kristalnim rešetkama, kao što su akustički talasi u anharmoničkim rešetkama, ali i jonski akustički talasi u plazmi.
Nelinearna Šredingerova jednačina ima važnu ulogu u teoriji nelinearnih talasa u nelinearnoj optici i fizici plazme.
Sinus-Gordonovu jednačinu je prvi upotrebio Edmond Bur 1862. godine, pri proučavanju površi sa negativnim zakrivljenjem. Jednačina je posle gotovo zaboravljena, dok je ponovo 1939. godine nisu primenili Frenkelj i Kontorova, u svojoj studiji o dinamici dislokacija u kristalima. Pošto sadrži i solitonska rešenja, od 70-tih godina se mnogo koristi. Interesantno je da ova jednačina poseduje solitonska (kink i antikink rešenje) i višesolitonska rešenja (od dvosolitonskih rešenja ove jednačine interesantna su rešenja oblika kinkova i/ili antikinkova, koji kada se „sudare“ prolaze jedan kroz drugi i jedini efekat koji se pri tome opaža je fazni pomak dvaju solitona. Pošto sačuvaju svoj oblik, ovakav vid sudara solitona se zove elastičnim. Drugi vid dvosolitonskog rešenja je upareno kink-antikink rešenje, tzv. brizer. Postoji i kvantna verzija ove jednačine koja je našla primenu u kvantnoj teoriji polja.
D. Čevizović
Kompletni tekstove sa slikama i prilozima potražite u magazinu
"PLANETA" - štampano izdanje ili u ON LINE prodaji Elektronskog izdanja
|
