FIZIKA

Pripremio: D. Čevizović

Simetrija
Vagnerovo zaveštanje

Vekovima, osećaj za simetriju se izgrađivao, da bi simetrija postala jedan od najznačajnijih principa sklada i osećaja za lepotu u umetnosti i u prirodnim zakonima. U ovom tekstu nas, međutim, neće interesovati subjektivan osećaj za simetriju, već njena povezanost sa fizičkim zakonima. Interesuje nas ne simetrija koja se pojavljuje u oblicima pojedinih predmeta već simetrija samih zakona fizike.

Principi simetrije ugrađeni su u temelje prirodnih zakona: oni su nerazdvojno povezani sa zakonima očuvanja i odgovarajućim invarijantnostima zakona fizike.

Grupa SU(2) i grupa rotacija u 3D Euklidovom prostoru SO(3)*

Grupa SU(2) je skup svih dvodimenzionalnih unitarnih matrica sa determinantom jednakom jedinici. Ova grupa potpuno je određena sa tri nezavisna parametra, za koje mogu da se uzmu bilo Kejli-Klajnovi parametri, bilo Ojlerovi uglovi.

Što se grupe rotacija tiče, neku rotaciju u trodimenzionalnom Euklidovom prostoru određuje osa oko koje se rotacija vrši i ugao za koji se rotacija vrši oko pomenute ose. Pošto rotacija “premešta” tačke prostora sa jednog na neko drugo mesto, kažemo da je ona operator u vektorskom prostoru. Operatori rotacije imaju dve vrlo važne osobine: oni su linearni operatori i ortogonalni operatori (održavaju rastojanja između dve zarotirane tačke, odnosno održavaju skalarni proizvod dva zarotirana vektora).

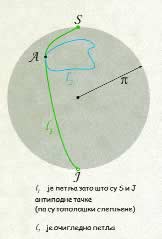
Grupa rotacija. Pošto su kvantnomehanička stanja zrakovi u Hilbertovom prostoru, Vigner je sa grupe rotacija SO(3) prešao na njoj univerzalno natkrivajuću grupu SU(2). Ireducibilne reprezentacije grupe SU(2) tada odgovaraju tipovima čestica. U ovoj grupi se na primer, spinori koji opisuju elektrone, kvarkove i neutrone pojavljuju sasvim prirodno. U pi-lopti postoje dve klase petlji. Ako iz svake klase odaberemo po jednu petlju, može se zapaziti da ne postoji nikakva glatka transformacija kojom bi se jedna petlja preslikala u drugu.

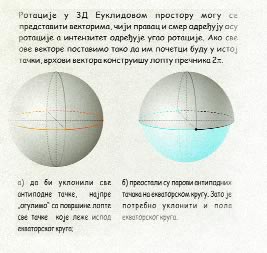Rotacije u 3D Euklidovom prostoru određene su pravom koja predstavlja osu rotacije i uglom za koji se rotacija izvrši. Drugim rečima, svakoj rotaciji može da se pridruži jedan vektor kolinearan sa osom rotacije, čiji intenzitet je jednak brojnoj vrednosti ugla za koji se rotacija vrši. Ako sve ove vektore premestimo tako da im je početak u jednoj tački, vrhovi ovih vektora grade loptu. To znači da svakoj tački (unutar i na površini lopte) odgovara jedna moguća rotacija, odnosno jedan element SO(3) grupe. Ipak, stvari nisu tako jednostavne: pošto je rotacija oko neke ose za ugao 180 stepeni (pi radijana) isto što i rotacija oko suprotne ose za ugao –180 stepeni (-pi radijana), bilo koje dve antipodne tačke na ovoj sferi zapravo predstavljaju istu rotaciju. Zato sve antipodne tačke treba “topološki slepiti” ili što je jednostavnije zamisliti, ako od pomorandže želimo da napravimo pi-sferu, treba oguliti pomorandžu ispod ekvatorijalne kružnice (prikazane narandžastom bojom), ali tako da kružnica ostane na pomorandži. Pošto i na ekvatorijalnoj krivoj postoje parovi antipodnih tačaka, treba ukloniti i pola ekvatorijalne kružnice. “Oguljeni” delovi pomorandže predstavljeni su plavom bojom, i ovo što je preostalo posle “guljenja” najbliže je onome što se naziva pi-loptom.

Grupu SO(3) čini skup svih rotacija u trodimenzionalnom Euklidovom prostoru - odatle (3) u nazivu grupe - pri čemu je grupna operacija uzastopna primena dve rotacije. Ako izaberemo neki ortonormirani bazis u vektorskom prostoru, rotacije se u ovom bazisu reprezentuju ortogonalnim matricama; odatle ono O u nazivu grupe. Determinanta ovih matrica može biti +1 ili –1. Podskup ortogonalnih matrica kojima je determinanta +1 predstavlja prave rotacije u vektorskom prostoru, zove se specijalna ortogonalna grupa i označava se sa SO. Svaka rotacija u 3D prostoru potpuno je određena sa tri parametra (smer ose, njen pravac i ugao za koji se izvodi rotacija), pa ove matrice imaju tri parametra. Pošto se svaki od njih može neprekidno (glatko) menjati, grupa SO(3) je Lie-jeva grupa.

Mnoge osobine SO(3) grupe koje su veoma važne za fiziku, najlakše se vide iz topoloških osobina pi-lopte (to je mnogostrukost koja u parametarskom prostoru opisuje grupu rotacija). Šta je to pi-lopta, može se naslutiti iz slike...

Svake dve tačke koje pripadaju pi-lopti mogu se spojiti krivom koja iz nje ne izlazi. To znači da je pi-lopta povezana, a njene ireducibilne reprezentacije su određene ireducibilnim reprezentacijama odgovarajuće Lie-jeve algebre. Ako međutim posmatramo petlje iz neke tačke, zapazićemo da postoje dve različite klase koje se ne mogu nekom neprekidnom transformacijom prevesti jedna u drugu. To znači da prostor parametara nije prosto povezan, već je dvostruko povezan, a ova osobina SO(3) grupe direktno je povezana sa postojanjem polucelobrojnih spinova elementarnih čestica.

Korisni primeri petlji iz ovih dveju klasa predstavljaju sledeće dve petlje: prva se može konstruisati kao pravolinijska putanja koja polazi sa “severnog” pola (iz tačke S) i kroz centar pi-lopte završava na “južnom” polu (u tački J). Ovo jeste petlja jer su tačke S i J antipodne, odnosno to je jedna te ista tačka. Dobijena petlja pripada istoj klasi kojoj pripada i petlja l1 sa slike. Petlje iz ove klase ne mogu se stisnuti nekakvom topološkom deformacijom u jednu tačku. Ovakva petlja zapravo reprezentuje rotacije oko z-ose za sve uglove od 0 do 2pi. Klasi l2 bi pripadala petlja koja polazi iz tačke S i kroz centar stiže u tačku J, da bi se ponovo kroz centar vratila u tačku S. Ovakva petlja se može stisnuti u jednu tačku. Ovoj petlji odgovaraju rotacije oko z-ose za uglove od 0 do 4pi.

Ovakva, na prvi pogled suvoparna, neprivlačna matematika u rukama majstora matematičke i teorijske fizike predstavlja moćno oruđe (moćno bar koliko i dobro osmišljen i izveden eksperiment) koje na iznenađujući način može osvetliti tamne uglove prirode i na svetlo izvući do tada neslućene povezanosti, dajući im oblik jednostavnih fizičkih zakona. Ilustrativan primer predstavlja upravo skicirana veza kvantne teorije uglovnog momenta i teorija reprezentacija SO(3) grupe, koja na elegantan, geometrijski način (što u neku ruku deluje kao magija) objašnjava polucelobrojne spinove (bolje rečeno, ukazuje da mora postojati nešto kao što je polucelobrojni spin) i čijem razvoju je Vigner dao nemerljiv doprinos.

Teorija simetrije i nuklearna fizika

Primenom teorije grupa Vigner je objasnio mnoge osobine atomskih spektara, a neke od njih i teorijski predvideo. Pokazao je, na primer, da se brojna selekciona pravila mogu objasniti kao jednostavne posledice simetrije posmatranog fizičkog sistema. Laporteovo pravilo koje dopušta dipolne prelaze elektrona samo između parnog i neparnog stanja se, na primer, može shvatiti kao posledica zakona održanja parnosti talasne funkcije. Kao još jedan važan primer treba pomenuti Vigner-Ekartov teorem, koji je i dan danas nezaobilazna lekcija u svakom kursu primene teorije simetrije u fizici atoma, molekula i čvrstog stanja.

Tridesetih godina prošlog veka Vigner je razvijao teoriju simetrije u nuklearnoj fizici. Iako se bavio matematičkom fizikom, Vigner je na prvom mestu ostao fizičar i nije se ustezao da razmatra i približne simetrije nekog fizičkog sistema. On je odigrao važnu ulogu u razvoju koncepta simetrije izotopskog spina (izospina), približne simetrije jake interakcije. Kasnije je ovu simetriju proširio na grupu SU(4) koja sadrži na netrivijalan način i izospin i rotacionu simetriju. Kombinovanje unutrašnjih simetrija (impuls neke čestice ili njen moment impulsa su vektorske fizičke karakteristike, pri čemu se ovi vektori mogu predstaviti u vektorskom prostoru koji je vezan za prostor u kojem se ta čestica nalazi. Međutim spin i još neke druge karakteristike čestica, su vezane za prostor parametara a ne prostor u kojem posmatrač i čestica postoje. Ovaj prostor se zato zove unutrašni prostor, a stanja čestica u ovom prostoru takođe mogu ispoljavati neku simetriju. To je unutrašnja simetrija - prim. prev.) sa simetrijama prostor-vremena i njihovo objedinjavanje u jednu grupu predstavljao je hrabar korak. Isti pristup su 60-tih godina primenjivali fizičari koji su se bavili elementarnim česticama, kada su pokušali da kombinuju Lorencovu grupu (pošto su elementarne čestice relativistički objekti - prim. prev.) i unutrašnje simetrije, ali sa mnogo manje uspeha.

Vigner je dao veliki pedagoški doprinos savremenoj fizici. Na njegovom radu je školovana generacija fizičara koja je primenjujući teoriju grupa imala zapaženu ulogu u razvoju atomske, nuklearne a kasnije i fizike elementarnih čestica.

Reprezentacije Poenkareove grupe

Krajem 30-tih godina, Vigner se posvetio izučavanju vremenski zavisnih simetrija, grupa simetrija koje uključuju invarijantnost na translacije u vremenu: nehomogene Lorencove grupe, koje se ponekad u literaturi nazivaju i Poenkareove grupe. Poenkareovu grupu do tada nisu ozbiljno razmatrali ni matematičari ni fizičari. Tada je i objavio epohalni rad The Unitary Representations of the Inhomogeneous Lorentz Group (E.P.Wigner, Ann. Math., 40, 149 (1939)). U ovom radu dat je potpun odgovor na pitanje šta predstavljaju unitarne reprezentacije Poenkareove grupe i kakav je njihov fizički značaj. Vigner je pokazao da su u relativističkoj kvantnoj mehanici Poenkareove transformacije predstavljene vernom reprezentacijom njene univerzalno natkrivajuće grupe ISL(2,C), te je dao potpunu klasifikaciju njenih ireducibilnih reprezentacija i sve ih eksplicitno konstruisao. Metoda kojom je ovo uradio je bila genijalna.

Vigner je pokazao da se ireducibilne reprezentacije ove grupe mogu označiti svojstvenim vrednostima dvaju Kazimirovih operatora; jedan predstavlja masu dok je drugi povezan sa ugaonim momentom čestice. Da bi se konstruisala reprezentacija dovoljno je da se razmotri podgrupa (mala grupa) transformacije koja četverovektor impulsa ostavlja invarijantnim pa se svaka Lorencova transformacija može napisati kao proizvod takozvanih bustova i elemenata male grupe. Stoga postoje dva tipa reprezentacije:

1) Masena reprezentacija: M > 0. Ovde je mala grupa prosto grupa rotacija, pa postoji jedna ireducibilna reprezentacija za svaku od ireducibilnih reprezentacija grupe SU(2).

2) Bezmasena reprezentacija: M = 0. Ovde je mala grupa dvodimenzionalna Euklidova grupa koju čine dve translacije i jedna rotacija dvodimenzione ravni. Jedina konačnodimenziona reprezentacija ove grupe je jednodimenzionalna, u kojoj translacije deluju trivijalno.

Vignerova analiza je jasno pokazala da se bezmasene čestice sa spinom u osnovi razlikuju od čestica sa masom. Zapravo, Vigner je uspeo da razvije kompletan alat koji omogućuje klasifikaciju svih elementarnih čestica. Osim toga, on obezbeđuje i definiciju elementarne čestice: prema Vigneru svakoj elementarnoj čestici korespondira ireducibilna reprezentacija Poenkareove grupe. (Time je na osnovu simetrije u svetu elementarnih čestica urađeno isto ono što je u periodnom sistemu elemenata svojevremeno uradio Dimitrij Mendeljejev - prim. prev.). Vigner je svoju definiciju elementarne čestice uzimao veoma ozbiljno. Za vreme jedne diskusije u Prinstonu, Vigner je primetio da je veoma teško prihvatiti fizičku realnost kvarkova, pošto se oni ne mogu opservirati kao asimptotska stanja i nisu u skladu sa njegovom definicijom elementarne čestice. Nije promenio mišljenje čak ni kad su mu sagovornici predočili da po njegovoj strogoj definiciji neutron nije elementarna čestica, pošto je nestabilan. Uprkos Vignerovoj definiciji, danas se smatra da kvarkovi postoje i da su fundamentalni konstituenti hadrona.

Značaj simetrije

Za svoj rad na otkrivanju i primeni fundamentalnih principa simetrije Vigner je 1963. godine dobio Nobelovu nagradu. U svečanom predavanju koje je održao prilikom dodele nagrade, ali i u svakoj drugoj prilici isticao je dalekosežan uticaj principa simetrije u prirodnim naukama. Ukazivao je da se razmatranje svakog fizičkog problema svodi na analiziranje početnih uslova (koji su proizvoljni, komplikovani i nepredvidljivi) i prirodnih zakona (koji opisuju pravilnosti nezavisne od početnih uslova). Uloga principa simetrije je donekle slična ulozi prirodnih zakona (slika). Oni predstavljaju pravilnosti koje se pojavljuju u prirodnim zakonima i koje su nezavisne od specifične dinamike. Zato je Vigner ukazivao da principi invarijantnosti obezbeđuju strukturu i koherentnost prirodnih zakona, baš kao što i prirodni zakoni obezbeđuju strukturu i koherentnost skupa događaja (npr. tabeliranih podataka merenih u nekom eksperimentu).

Zaista, danas je nezamislivo da je moguće postići neki veći napredak u otkrivanju prirodnih zakona bez postojanja, uočavanja i primene određenih simetrija. Tako je na primer mogućnost ponavljanja eksperimenata na različitim mestima i u različitim trenucima zasnovana na invarijantnosti prirodnih zakona na translacije u prostoru i vremenu. Bez pravilnosti ugrađenih u zakone fizike nemoguće je shvatiti smisao fizičkih događaja; bez pravilnosti u prirodnim zakonima nemoguće je i otkrivanje samih zakona.

Jezgro ovog teksta čini članak objavljen u časopisu Physics Today, Symmetry in Physics: Wigner's Legacy, dec. 1995., str. 46-50, autora Davida J. Grosa, profesora fizike sa Princeton University iz Prinstona.

Autor se zahvaljuje dr Zoranu Popoviću, iz INN Vinča, i dr Dušku Borki i mr Vesni Jovanović Borki, iz INN Vinča, na sugestijama bez kojih ovaj tekst svakako ne bi imao ovakav oblik.

D. Čevizović