FIZIKA

Pripremio: Dalibor Čevizović

Svet s druge strane kvanta

Svetom molekula, atoma i elementarnih čestica upravljaju zakoni kvantne mehanike. Ponašanje ovako malenih delića materije ne liči ni na šta sa čime se svakodnevno susrećemo. Naše svakodnevno iskustvo kazuje nam da se materija u prirodi javlja ili u obliku tela koja su građena od manjih ili većih delića a koji se pokoravaju Njutnovim zakonima mehanike, ili su to talasi čije je ponašanje određeno zakonima fizike talasa. Međutim, kvantni sistemi se ne ponašaju ni kao bilijarske kuglice, ni kao tela okačena na elastičnu oprugu, ni kao talasi na vodi ili zvučni talasi. Bukvalno, njihovo ponašanje je potpuno različito od bilo čega što smo videli u svom okruženju.

Demokrit iz Abdere

Kako je nastao i kako je ustrojen svet koji nas okružuje? Koji zakoni upravljaju prirodnim pojavama? Iz čega je sazdana materija i koji su njeni osnovni gradivni elementi? Da li materija može da se deli na beskonačno sitne deliće ili se, pri mrvljenju nekog tela, jednom mora doći do njegovih najsitinijih delića? Kako se ovi delići međusobno drže zajedno? Ova pitanja su od davnina imala neodoljivu draž. Njima su se ljudi bavili čak i pre nastanka civilizacije i pisane istorije.

Tražeći odgovore, drevni mudraci su stvorili prve teorije o nastanku sveta i njegovom ustrojstvu: kosmogonijske mitove, u kojima je bilo utkano svo onovremeno znanje. Bilo je potrebno da prođe nekoliko milenija pa da se u antičkom svetu pitanje o strukturi materije postavi na savremen način. Tako su Leukip iz Mileta, Demokrit iz Abdere (oko 420. p.n.e.) smatrali da materijalna tela nisu beskonačno deljiva i da se pri deljenju nekog tela na kraju dolazi do njegovih elementarnih delova: do atoma. Platon (428-348. p.n.e.) je u Timeju raspravljao o načinu na koji su elementarni delići materije povezani. Smatrao je da su atomi koji grade različita tela različitih oblika, te da su međusobno povezani kukicama. Moglo bi se reći da ova ideja leži u osnovi moderne teorije međumolekularnih i međuatomskih sila. I stvaraoci kosmogonija starih civilizacija i antički filozofi oslanjali su se na najmoćnije oruđe kojim su raspolagali: iskustvo koje su stekli posmatranjem prirode.

Brza industrijalizacija u 19. veku podstakla je razvoj prirodnih nauka, pre svega termodinamike, hemije, fizike niskih temperatura i elektromagnetizma. Najednom su počela da iskrsavaju pitanja na koja klasična fizika nije mogla da pruži odgovore.

Da bi objasnio zakone zračenja crnog tela, Maks Plank je početkom 20. veka postavio kvantnu hipotezu: atomi koji grade neko telo emituju ili apsorbuju energiju u tačno određenim energijskim porcijama, kvantima energije. Do tog trenutka kontinualnost promena u prirodi nikada nije bila dovođena u pitanje. Pojava diskontinualnosti u procesima na atomskom nivou značila je potpuni raskid sa tradicionalnim shvatanjima. Danski fizičar Nils Bor (Niels Bohr, 1885-1962.) stvara prvu teoriju atoma kojom objašnjava Raderfordove (Ernest Rutherford, 1871-1937.) rezultate rasejanja elektrona na atomima zlata. Ispostavilo se da je ovo bio pun pogodak! Primenom Borove teorije objašnjeni su emisioni spektri atoma vodonika, postavljeni su temelji kvantne hemije, objašnjen periodni sistem elemenata... Otkrivanje zakona atoma u narednim godinama uglavnom je išlo smernicama koje je postavio Bor. Međutim, teškoće koje su se javljale pri pokušajima shvatanja zakonitosti mikrosveta ispoljavale su se sve oštrije. Komptonovo otkriće da se pri rasejanju svetlosti na slobodnim elektronima menja njena talasna dužina moglo se objasniti primenom korpuskularnog modela svetlosti, koji je postavio Ajnštajn pri objašnjenju fotoefekta. S druge strane postojalo je mnoštvo eksperimenata u kojima je svetlost ispoljavala svoju talasnu prirodu.

Postepeno, istraživači su se privikavali na činjenicu da su slike i pojmovi preneseni iz klasične fizike u svet atoma samo napola tačni. Tek se 1924. godine počeo nazirati izlaz iz ovakve maglovite situacije. Posle jednog neuspešnog pokušaja da proračuna putanje elektrona u atomu vodonika, Verner Hajzenberg (Werner Heisenberg, 1901- 1976.) je naslutio da one i nemaju fizički smisao. Smisla imaju samo veličine koje se mogu meriti u eksperimentu. U ovom slučaju su to frekvencije i intenziteti spektralnih linija svetlosti koje atom emituje pri prelazima elektrona iz jednog u neko drugo stanje. Nakon nekih nedoumica Hajzenberg je uspeo da formuliše zaokruženu, unutrašnje povezanu matematičku zgradu koja je omogućavala da se uspešno izračunaju energije stacionarnih stanja atoma ili verovatnoće prelaska iz jednog stanja u drugo: stvorena je matrična mehanika. Ali i dalje nije bilo jasno kako je matrična mehanika povezana sa jezikom svakodnevne fizike.

Jednom prilikom je Ajnštajn Hajzenbergu ukazivao da se putanja elektrona može videti u maglenoj komori i da je besmisleno reći da ona ne postoji. Hajzenberg je i sam bio svestan ovog problema i sve napore usmerio je na ovo pitanje. Uskoro mu je sinulo da ono što se u maglenoj komori vidi nije putanja čestice, već diskretan niz kapljica čiji položaj je manje ili više tačno određivao mesta gde se elektron nalazio (pošto je formirana kapljica mnogo veća od čestice, ona samo približno govori o njenom položaju). Ispravno postavljeno pitanje moralo bi u stvari glasiti: da li je moguće da se u kvantnoj mehanici prikaže situacija u kojoj se elektron sa određenom netačnošću nalazi na nekom datom mestu i pri tome ima, opet sa nekom netačnošću, neki unapred dat impuls i mogu li se te netačnosti toliko smanjiti da se sa eksperimentom ne dospe u ćorsokak? Dodatni proračuni su pokazali da je to ostvarivo. Rođene su Hajzenbergove relacije neodređenosti koje kažu da proizvod neodređenosti položaja kvantne čestice i neodređenosti njenog impulsa mora biti veći ili jednak Plankovoj konstanti: . Kasnije je Bor uspeo da poveže ove relacije sa svojim principom komplementarnosti.

U isto vreme u Beču je Ervin Šredinger (Erwin Schrödinger, 1887-1961.), na osnovu De Broljevih ideja o talasnoj prirodi čestica, razvio drugačiju formulaciju kvantne mehanike: talasnu mehaniku. On je u svojoj teoriji stacionarna stanja elektrona poredio sa stojećim talasima u elastičnim strunama. Svakoj kvantnoj čestici je pridružen talas materije, koji je u prvim interpretacijama bio opažajno zbivanje u prostoru i vremenu, slično kao kod elektromagnetnih i zvučnih talasa. Talasna mehanika je omogućavala da se, na relativno jednostavan način, izračunaju neki problemi koji bi se primenom matrične mehanike teško rešili. Iako su u početku mnogi fizičari Šredingerovu talasnu mehaniku prihvatili sa olakšanjem, vremenom su se pojavile teškoće pri fizikalnom tumačenju ove teorije. Ispostavilo se da je prostorno-vremensko opisivanje kvantnih događaja nemogućno. Kasnije će Šredingerovi talasi biti interpretirani kao talasi verovatnoće: kvadrat talasne funkcije pridružene nekoj kvantnoj čestici predstavlja verovatnoću njenog nalaženja u datoj prostorno-vremenskoj tački.

Čudni svet kvantnih pojava

Da bi se pojmilo koliko je ponašanje kvantnih sistema različito od našeg svakodnevnog iskustva, zgodno je da se razmotri kakvo ponašanje za neki fizički sistem predviđa klasična fizika, a zatim ga uporediti sa onim koje predviđa kvantna fizika. U tu svrhu često se osmišljavaju jednostavni misaoni eksperimenti, koji ipak sadrže osnovne karakteristike kvantnog ponašanja sistema. Razmatranjem ovakvih misaonih eksperimenata na Solvejevim kongresima, koji su se počev od 1927. godine održavali svake treće godine u Briselu, kroz borbu mišljenja raščišćavani su nerešeni problemi kvantne fizike.

Difrakcija svetlosti na dva otvora

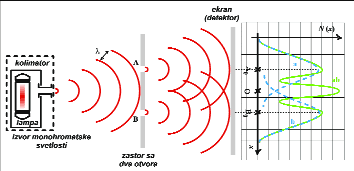
U klasičnoj fizičkoj optici dobro je poznata difrakcija svetlosti kroz dva otvora, Jangov eksperiment, objavljen 1802. godine (Thomas Young). Difrakciona slika koja se u ovom eksperimentu dobija na zastoru jedan je od najprostijih primera interferencije elektromagnetnih talasa. Šema eksperimenta prikazana je na slici 1. Monohromatska svetlost koju emituje tačkast izvor nailazi na zapreku na kojoj se nalaze dva malena otvora. Rastojanje između otvora pri tome mora biti reda veličine talasne dužine svetlosti koja nailazi na njih. Sada ovi otvori, po Hajgensovom principu, postaju izvori koherentnih (ovo znači da je fazna razlika između zrakova koji interferiraju na zastoru vremenski nepromenljiva) sfernih talasa koji se međusobno superponiraju. Difrakciona slika se posmatra na zastoru. Nju čini niz jače ili slabije osvetljenih tačaka koje se nalaze na izvesnom međusobnom rastojanju. Prostorna raspodela intenziteta osvetljenosti dodatno je prikazana na grafikonu sa strane (intenzitet talasa u nekoj prostornoj tački je proporcionalan kvadratu njegove amplitude i mera je gustine energije talasa).

Modifikujmo Jangov eksperiment tako što ćemo u prvoj fazi eksperimenta držati otvorenim samo otvor A, a otvor B zatvoren. Na ekranu ćemo dobiti duž x ose raspodelu intenziteta prikazana krivom a. U drugoj fazi eksperimenta zatvorimo otvor A i otvorimo otvor B. Na ekranu dobijamo raspodelu b. U trećoj fazi eksperimenta, kada su otvorena oba otvora, dobija se raspodela intenziteta ab. Interesantno je da se na sredini zastora nalazi svetla interferenciona tačka, iako direktno ispred nje nema otvora kroz koji bi svetlost mogla da stigne! Ovo je posledica talasne prirode svetlosti, tj. osobine da talas može da se prostire i iza postavljene zapreke (difrakcija).

Izvor klasičnih čestica ispred zastora sa dva otvora

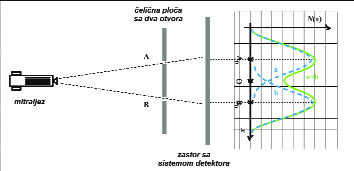
Ako bismo uradili analogan eksperiment sa klasičnim česticama (npr. postavili mitraljez, a ispred njega čeličnu neprobojnu ploču na kojoj se nalaze samo dva podjednaka otvora), rezultat bi bio dramatično drugačiji (slika 2.). U ovom eksperimentu bi intenzitetu svetlosti u nekoj tački na zastoru odgovarao broj čestica u posmatranoj tački zastora. I u ovom slučaju bi poneki metak zalutao u odnosu na pravolinijsku putanju i našao se na delu zastora koji je zaklonjen, ali se ovo može objasniti rikošetom metka na stenci otvora. U svakom slučaju, što su otvori uži, to je rasturanje pogodaka manje, odnosno pogodci su bolje grupisani naspram otvora kroz koji su prošli. U prvoj fazi eksperimenta, kada je otvoren samo otvor A dobili bi raspodelu pogodaka predstavljenu krivom a (analogno se u drugoj fazi eksperimenta dobija raspodela b). U trećoj fazi eksperimenta, sa oba otvora otvorena, dobijena raspodela pogodaka odgovara algebarskom zbiru krivih a i b: dobija se kriva a+b.

Eksperiment sa izvorom elektrona

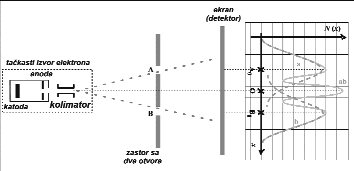
Šta će se desiti ako u Jangovom eksperimentu izvor svetlosti zamenimo izvorom elektrona? Kakvu raspodelu elektrona možemo očekivati na zastoru? Provedimo sve tri faze eksperimenta i pogledajmo dobijene raspodele.

Pošto su elektroni čestice, a svaka čestica, bio to elektron ili mitraljeski metak, sa tačke gledišta klasične fizike ima svoju putanju, očekujemo da se slika dobijena na ekranu kvalitativno ne razlikuje od rezultata postignutih u opisanom eksperimentu sa mitraljezom. Ako je neki elektron stigao do zastora očekujemo da je prošao ili kroz otvor A ili kroz otvor B (a nikako kroz oba). Distribucione krive a i b dobijene u prve dve faze eksperimenta ne protivureče ovoj pretpostavci. Međutim, kriva ab koja je dobijena u trećoj fazi eksperimenta, kada su otvorena oba otvora, je u oštroj suprotnosti sa našim očekivanjem. Naime, pošto su elektroni čestice, raspodela elektrona na zastoru bi trebala biti analogna raspodeli a+b. Zastor ne razlikuje da li je elektron prošao kroz otvor A ili otvor B i detektori na zastoru detektuju zbir svih ovih čestica. Da bi se bolje sagledalo koliko se raspodela ab razlikuje od raspodele a+b, treba zapaziti sledeće detalje:

a) u tački koja se nalazi na sredini između tačaka A0 i O ordinata krive ab ne samo da je manja od ordinate krive a+b, nego je čak osetno manja od odgovarajuće ordinate krive a. To bi, na osnovu naše pretpostavke o klasičnim trajektorijama, značilo da broj elektrona koji stižu u dotičnu tačku na zastor prolazeći kroz otvor A opadne (!) kada se otvori i otvor B. b) U tački O ordinata krive ab je više nego dva puta veća od ordinate krive a+b. Znači, ako su oba otvora istovremeno otvorena, u tačku O stiže mnogo više elektrona nego što je ukupan broj elektrona koji prođu kroz otvor A (sa zatvorenim otvorom B) i elektrona koji prođu kroz otvor B (sa zatvorenim otvorom A).

Poredeći raspodelu elektrona sa difrakcionom slikom u Jangovom eksperimentu, uočava se njihova velika kvalitativna sličnost (pri tome jačina osvetljenosti u Jangovom eksperimentu odgovara broju upadnih elektrona). Nameće se zaljučak da elektroni kroz otvore na prepreci prolaze kao talasi! Ako su oba otvora otvorena, onda elektroni prolaze istovremeno i kroz otvor A i kroz otvor B, da bi na drugom zastoru interferirao sa samim sobom! U pojedinim tačkama je ta interferencija konstruktivna pa je ovde verovatnoća detekcije elektrona veća, dok je na drugim mestima interferencija destruktivna, pa je verovatnoća detekcije elektrona u ovim tačkama manja.

Da bi otklonili sumnju da se ovde možda radi o nekakvoj interakciji između elektrona koji su prošli kroz otvor A sa elektronima koji su prošli kroz otvor B, zamislimo da iz izvora emitujemo jedan po jedan elektron, pri čemu je vreme između dve emisije dovoljno dugo tako da je prvi elektron već prošao kroz otvor kad se naredni emituje. Eksperiment vršimo sve dok se u pojedinim tačkama na zastoru ne akumulira dovoljno velik broj čestica. Dobijaju se potpuno isti rezultati kao i sa intenzivnim snopom i kratkim vremenom ekspozicije.

Kojim putem ide elektron?

Pokušajmo da napravimo eksperiment koji će nam reći kojim putem se elektron kretao, odnosno kroz koji otvor je prošao. Dodamo li u našu aparaturu jak izvor svetlosti neposredno iza zastora, a između otvora A i B, moći ćemo detektovati kroz koji otvor je elektron prošao. Naime, naelektrisana tela rasejavaju svetlost kojom su obasjana, pa kad elektron priđe našem detektoru, on će rasejati nešto svetlosti, što ćemo videti kao odbljesak u blizini otvora kroz koji je čestica prošla. Ako, na primer, elektron prođe kroz otvor B (kao na slici 4.) videćemo odbljesak u blizini ovog otvora. Kada bi elektron istovremeno prošao kroz oba otvora, videli bismo dva istovremena odbljeska, jedan kraj otvora A, a drugi kraj otvora B. Šta bi rekao ovakav eksperiment?Eksperimentator koji bi pratio eksperiment video bi odbljeske ili kraj jednog ili kraj drugog otvora, nikad istovremeno kraj oba! Znači, elektron ima svoju putanju i prolazi samo kroz jedan otvor. No - gle iznenađenja! - raspodela elektrona na zastoru bi bila (kao što je prikazano na slici 4.) a+b! U eksperimentu u kojem je moguće odrediti položaj elektrona interferencija nestaje! Uklonimo li izvor svetlosti, elektroni ponovo formiraju interferencionu sliku!

Šta se desilo sa elektronom? Da li se on pred zastorom cepa (slično talasu) na dva dela i prolazi istovremeno kroz oba otvora ili pak prođe kao i svaka čestica jednom od dveju mogućih putanja? Ovakvo pitanje zapravo nema smisla. Ono pretpostavlja da se u priodi nešto dešava nezavisno od posmatrača (ova pretpostavka uvek prećutno postoji u klasičnoj fizici), tj. da se procesi u kvantnom svetu mogu odvojiti od posmatrača i eksperimentalne aparature. Međutim, u mikrosvetu posmatrač i kvantni objekt čine nerazdvojnu celinu. U kvantnom svetu ne možemo prosto slušati šta priroda govori a da ona to govori slušali mi ili ne! Mi postavljamo pitanja, a priroda daje odgovore. Pri tome je, kao što se često kaže, pitanje već pola odgovora. U slučaju našeg eksperimenta, kad smo merili talasni aspekt elektrona (i na zastoru imali interferencionu sliku) čestični aspekt je ostao neodređen, tj. neostvaren. Nasuprot tome, mereći čestični aspekt elektrona, njegova talasna priroda ostaje neostvarena!

U kvantnoj mehanici je ovo poznato kao Hajzenbergov princip neodređenosti. On kazuje da svaki kvantni sistem poseduje niz osobina od kojih su dve na neki način antipodi jedna drugoj, tj. u takvom su međusobnom odnosu da merenje jedne od njih drugu nužno čini neodređenom. Takva dva aspekta Bor je nazvao komplementarnim.

Epilog

Opisani eksperimenti ukazuju koliko je kvantni svet drugačiji od sveta kakav poznajemo. Sada je već moguće naslutiti kakve su poteškoće imali pioniri kvantne fizike u razumevanju problema kojim su se bavili. Razumljiva je i nemogućnost opisa kvantnih sistema predstavama koje vuku korene iz našeg svakodnevnog iskustva. S druge strane, ona je dovela do revolucije u drugim prirodnim naukama, u tehnici i industriji i, u poslednje vreme, medicini, snažno je uticala na pojavu novih filozofskih pogleda na svet. Promene koje nam je donela kvantna fizika daleko su dramatičnije od promena do kojih je došlo primenom otkrića koja su zasnovana na zakonima klasične mehanike, termodinamike, pa čak i elektromagnetizma. Sve ovo nas je podstaklo da prirodu sagledavamo na bitno drugačiji način nego što smo to činili do pojave kvantne fizike. Time postaje razumljiv njen uticaj na naš svakodnevni život, ali i na način razmišljanja i delovanja, odnosno na istoriju civilizacije 20. veka.

Dalibor Čevizović